[コンプリート！] ベクトル 平行四辺形 面積 公式 261957-ベクトル 平行四辺形 面�� 公式

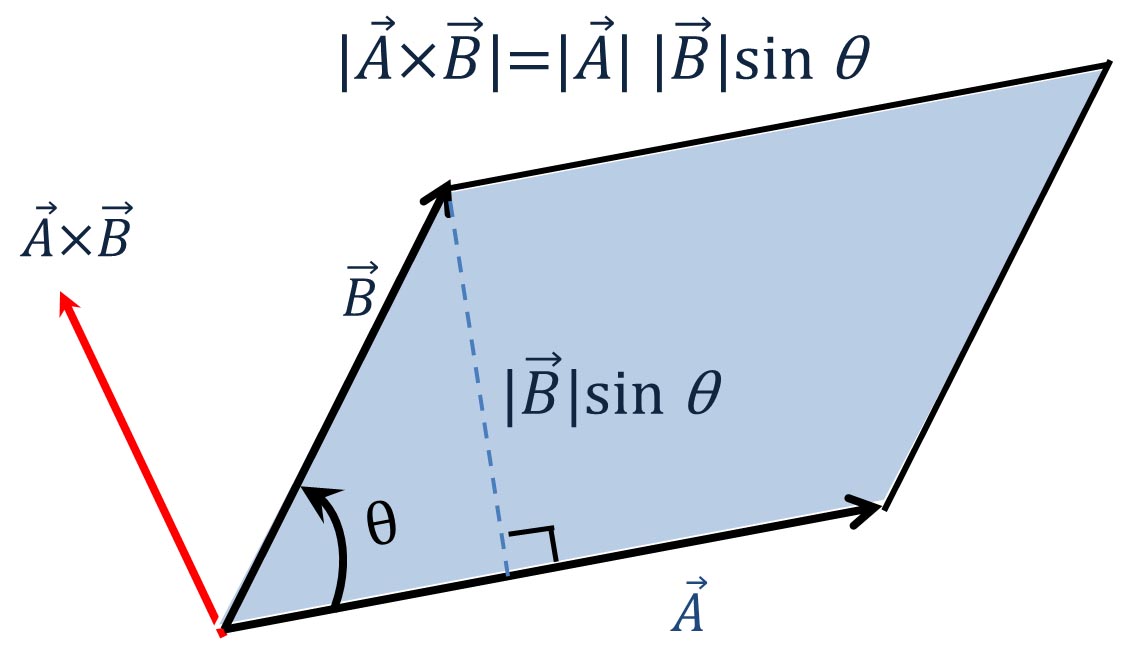
G36 平行四辺形の面積（空間の場合） ベクトル a =(a 1 ,a 2 ,a 3 ) と b =(b 1 ,b 2 ,b 3 ) が作る平行四辺形の面積 S は次の式で 与えられる。142注1 3次元空間での面積の公式 2つの3次元ベクトル が作る平行四辺形の面積 は、以下のようになる： は行列式である（ と書くと見づらいため）。 導出 導出は、内積の公式 を使うだけである。次に，ベクトル積の幾何学的な意味を考えよう．式(10)の演算は，図1のようになる． AとBで定まる平行四辺形の底面をAとすると，高さはjBjsin となる．従ってその面積 は，jAjjBjsin と直ちに分かる．これは，jA Bjに等しい．このことから，A Bのベク

新訂版序文の人 大類昌俊 Gvcuuchv 14 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで 平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な

ベクトル 平行四辺形 面積 公式

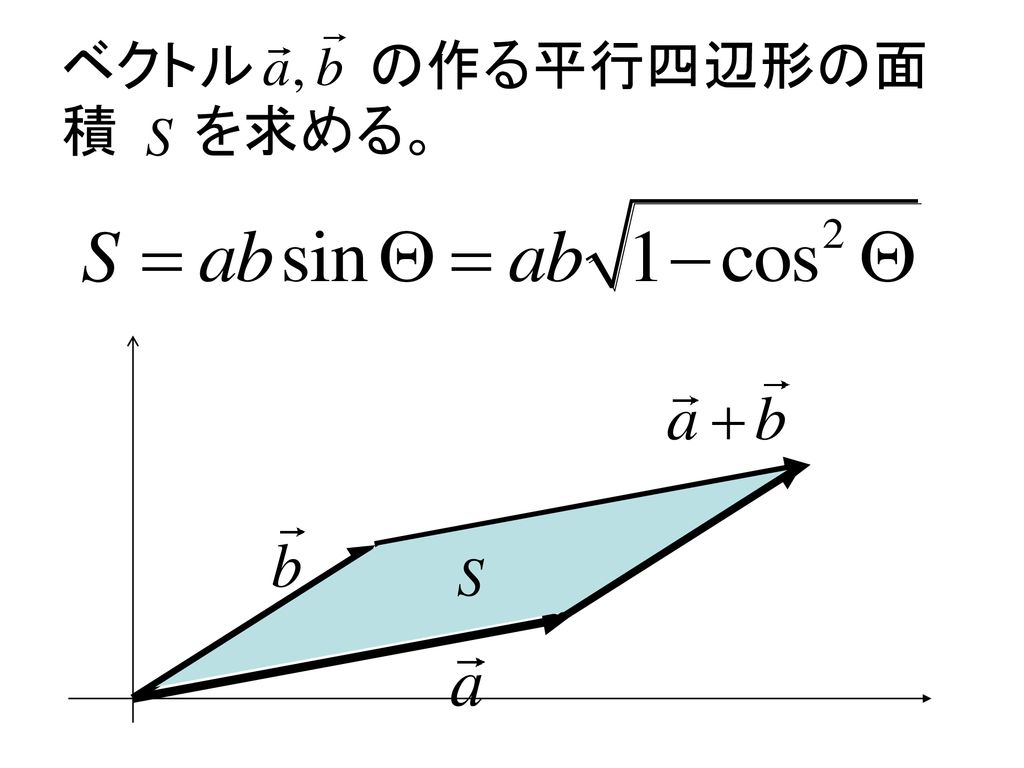
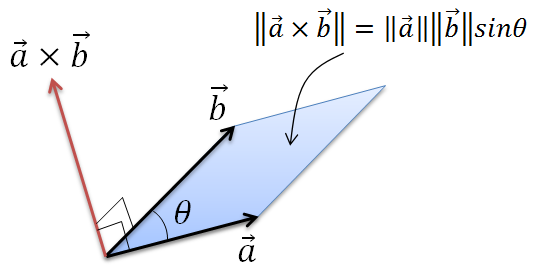
ベクトル 平行四辺形 面積 公式-例えば、𝒂と𝒃の外積𝒂× 𝒃は面積ベクトルである。𝒂と𝒃を2 辺にもつ平行四辺形を図形𝐷とし、図のような回転の向きを与 えると、図形𝐷に直交し、この平行四辺形の面積をノルム（大 きさ）とする正の向きのベクトルが𝒂× 𝒃だからである。1 三角形の面積の求め方 3 1 三角形の面積の求め方 頂点A;B;C の対辺の長さをそれぞれa;b;c とする 11 三角形の面積は平行四辺形の面積の半分 前節で述べたとおり, 三角形の面積は平行四辺形の面積の半分という考えから 底辺 高さ 2 (1) という公式が与えられる 執筆現在の学習指導要領によると

2

 ベクトルの外積 (裏技)による法線ベクトル・空間の三角形の面積・平行六面体の体積・四面体の体積 ベクトルの外積は受験数学最強の裏技の1つであり,\ 上級者は是非習得しておいてほしい 大学1年の最初に学習する程度の知識であり,\ 適用できる試験問題 14年 東大数学 理系第1問の解説連日の投稿です。今日から理系の問題の残りですね。14年の空間図形の問題です。 問題の分析三角関数、空間図形が登場し、面積を求める問題ですね。（2）ではαとβの条件が登場しますし、三角関数は必ず使いそうです。ベクトルの外積 の向きは，ベクトル の向きからベクトル の向きへ右ネジを回転させたとき，ネジの進む向きとする． ベクトルの外積 の大きさは， によってできる平行四辺形の面積に等しいものとする．

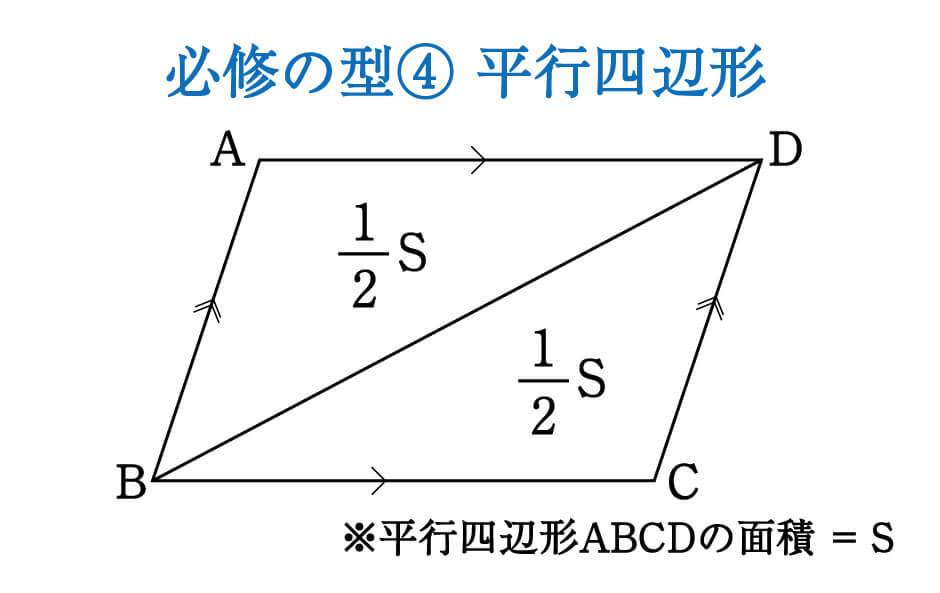
 あとは面積比を考えればおしまいですね。辺の比が分かっているので、面積比も求めることができます。 三角形 ABC の面積を S とすると、 $\mathrm{ BD }\mathrm{ DC }=54$ なので、三角形 ABD の面積は $\dfrac{5}{9}S$ 、三角形 ACD の面積は $\dfrac{4}{9}S$ となります。証明 はじめに 3次元ベクトル空間の任意のベクトルは、 3つの線形独立なベクトルによる線形結合によって表すことができる (「次元と同じ数だけある線形独立なベクトルは基底になる」を参考) 。 従って、 $0$ でない2つの線形独立なベクトル $\mathbf{a}$, $\mathbf{b}$ とそれらの間の外積線形性を用いることで 幾何的な問題を代数的に扱ってしまえる のが "線形性のマジック" 平行四辺形の面積と2次行列式

もつ平行四辺形を，この平行 6 面体の底面と考えると，この底面の面積 S はS ＝ h となる。 また，図13 に示すように，aとhのなす角φが，0 ≦φ π をみたすとき， a cos φは，a の終点から底面に下した垂線の長さ，つまり平行 6 面体 の高さl を表すことになるまた平行四辺形OAGDの面積と長方形OAG'D'の面積は等しい。つまり が成り立つ。 このときπ平面上のベクトルの方向に関して であることが言える。 このことと、｜｜：｜｜＝OB'：OC' であることを考慮すると、平行四辺形OB'D'C'と平四辺形OHJIは互いに 外積の定義 外積 a → × b → とは ①その向きが a → と b → に直交する方向で（右ネジの法則） ②その長さが「 a → と b → を2辺とする平行四辺形の面積」に等しい という性質を持ったベクトルのことを言います。

モデルの体積を計算する 試行錯誤

ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ

12 外積の公式は？ 13 外積の公式の覚え方; 平行四辺形の面積 まず, 2つのベクトル(ベクトルを横に書く悪習は辞めましょう) が張る平行四辺形の面積を考えよう 小学生でも習うこの公式 = (底辺) × (高さ) を思い出そう 底辺をとすると, これに対する高さは となる ここで, はとがなす角である すると, 面積は となるここではベクトル積 (クロス積、外積) の大きさは、2 つのベクトルが作る平行四辺形の面積に等しいということについて説明します。 以前の説明 ではベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が張る平行四辺形に、 そっと \(\ \overrightarrow{a} \times \overrightarrow{b}\\) と書いていました。

広島工業大学 工 情報 環境学部 A 10年問題4 Suugaku Jp

平行条件と面積と行列式 怜悧玲瓏 高校数学を天空から俯瞰する

 (6) 平行四辺形の面積・平行六面体の体積 外積を用いることで、ベクトルが張る平行四辺形の面積、ベクトルが張る平行六面体の体積を求めることができます。 (i) 平行四辺形の面積 2つのベクトル \( \vec{a} \), \( \vec{b} \) が張る平行四辺形の面積 \( S \) は\ こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の重心」 の座標・位置ベクトルの求め方や、その公式の証明、また重心の重要な性質を利用した面積比を求める問題などをわかりやすく解説していきます。 また、記事の後半では、三角形（別解2） 2つのベクトルの外積 はそれら2つに垂直な向きのベクトルになり，その大きさはベクトル でできる平行四辺形の面積に等しい． また，ベクトル でできる平行四辺形の面積は， と平行四辺形の高さ との積に等しいから 以上により （公式として覚える場合もある）

簡単公式 平行四辺形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

技術計算製作所 ベクトル解析 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Science Math Vector

平面の法線ベクトル a&b& の長さは、平行四辺形の面積 u S に等しい b & a & S ab && u a,b & が作る平行四辺形を含む面に 垂直で、長さが1のベクトルを法線ベク トルといい、 a b a b S a b1´ ´ a¨b ∥a∥∥b∥ ¯2) " ∥a∥2∥b∥2 ´pa¨bq2 " ˆÿn i"1 a2 i ˙ˆÿn j"1 b2 j2 外積が高校範囲の数学で役立つ場面は？ 21 平面の法線ベクトルの1つを求めるとき;

2

センター試験 数学ii B 第４問 ベクトルと中学受験 ふるやまんの算数塾

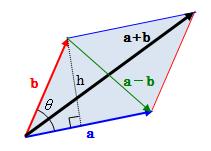
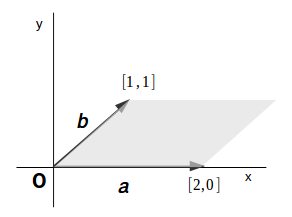
 ベクトルの内積を使って平行四辺形の面積を求める 同一平面上に原点 o 、点 a 、点 b があり、点 a の座標を (a₁,a₂ ）、点 b の座標を (b₁,b₂ ）とする。 abc の面積は、∠ aob=θ とすると、 であり、下図の平行四辺形 oacb の面積 s は である。 平行四辺形の面積の公式 平行四辺形の面積を求める公式には次の 2 通りがあります。 平行四辺形の面積の公式 平行四辺形の底辺を a 、高さを h 、斜辺を b 、底辺と斜辺のなす角を \theta とおくと、面積 S は \color {red} {S = ah} \color {red} {S = a b \sin\theta} (\textこの平行四辺形に外接する図のような平行四辺形CDEfの面積は、ベクトルAとBの張る平行四辺形の面積の2倍です。 （2重平行四辺形の面積の公式） この公式は上図から明らかですが、 以下で、この公式を、ベクトルの計算からも導き出してみます。

数学と音楽 年度岐阜大学文理共通数学２番 数学b ベクトルと平行四辺形の面積比 学習村の 国公立へ行こう

平行四辺形の面積を求めるある問題について 身勝手な主張

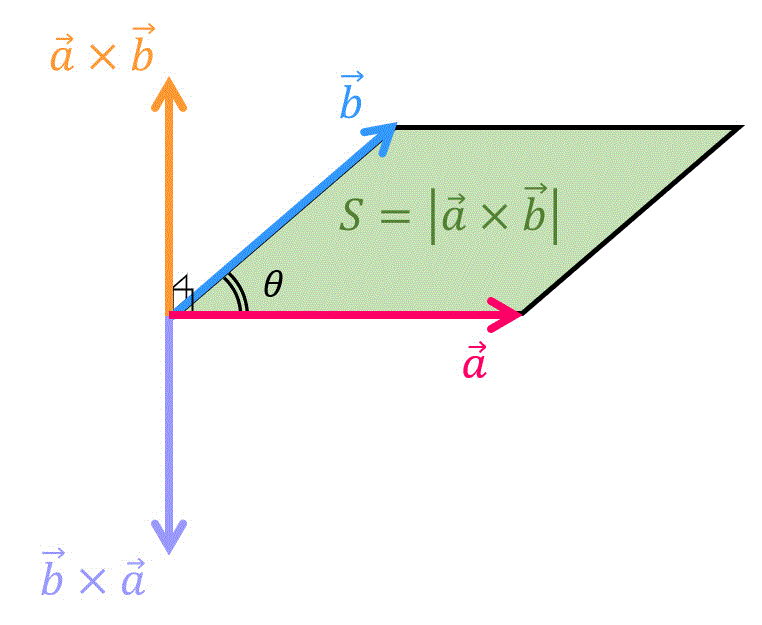
 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m2 面積と体積 21 平行四辺形の面積 n 次元ベクトルa,b の作る平行四辺形(右下図) の面積をS とすれば, a,b のなす角をθ (0 ď θ ď π) として, S2 " p∥a∥∥b∥sinθq2 " ∥a∥2∥b∥2! 外積の大きさは $\vec{a}$ と $\vec{b}$ からなる 平行四辺形の面積 と等しい。 外積の向きは、$\vec{a}$ から $\vec{b}$ 方向へ 右ねじ を回したときに進む向き。 以上、大切な情報が $3$ つ含まれています。

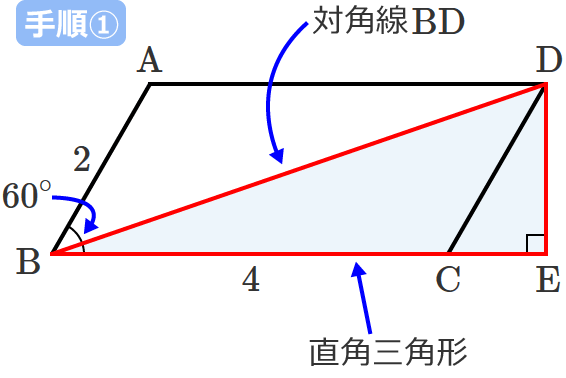
平行四辺形の対角線の長さの求め方

平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

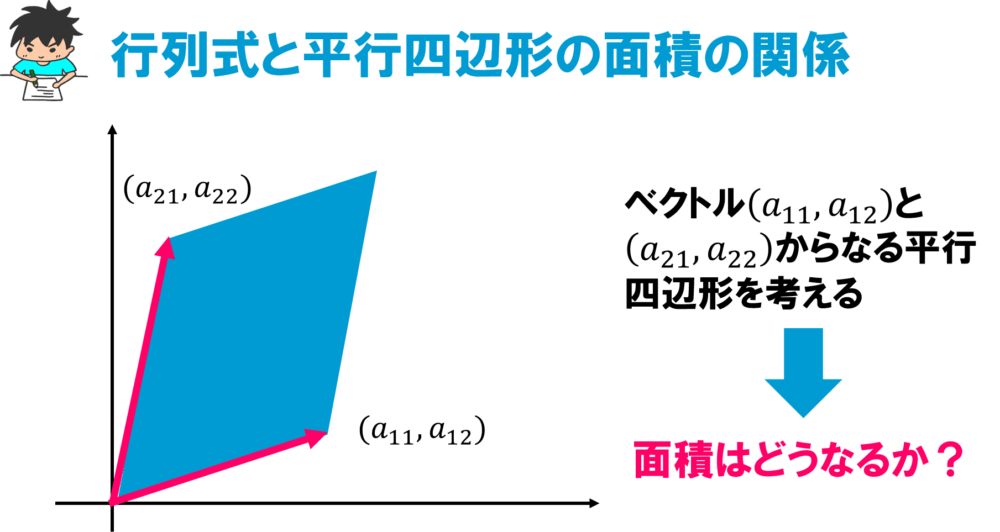
成分表示されたベクトルの内積公式の導出 — 双線形性を用いた "展開" によって基本ベクトル同士の内積に帰着する;< 平面のベクトルと行列式> 原点を始点とする2つのベクトル a = ³ a1 a2 ´ ，b = ³ b1 b2 ´ に対して，原点O(0，0)と3点 A(a1，a2)，B(b1，b2)，C(a1 b1，a2 b2) をとると，四角形OACB は平行四辺形となる。 この平行四辺形の面積をS とする。aとbの位置関係が 図1のような 平行四辺形も同様の公式で求められる 合同な三角形を二つ繋げると平行四辺形になるので，上記の公式から 1 2 \dfrac{1}{2} 2 1 を取った式で平行四辺形の面積を求めることができます。

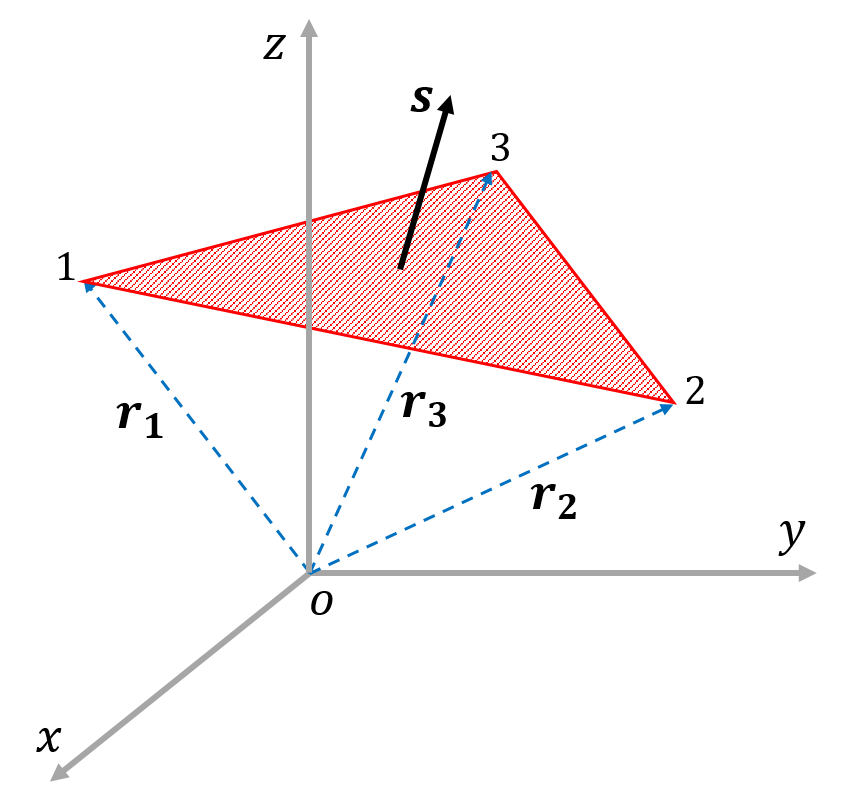
三角形の面積 科学技術計算ツール

平行四辺形の面積の２等分

ベクトルの外積と平行四辺形の面積 身勝手な主張

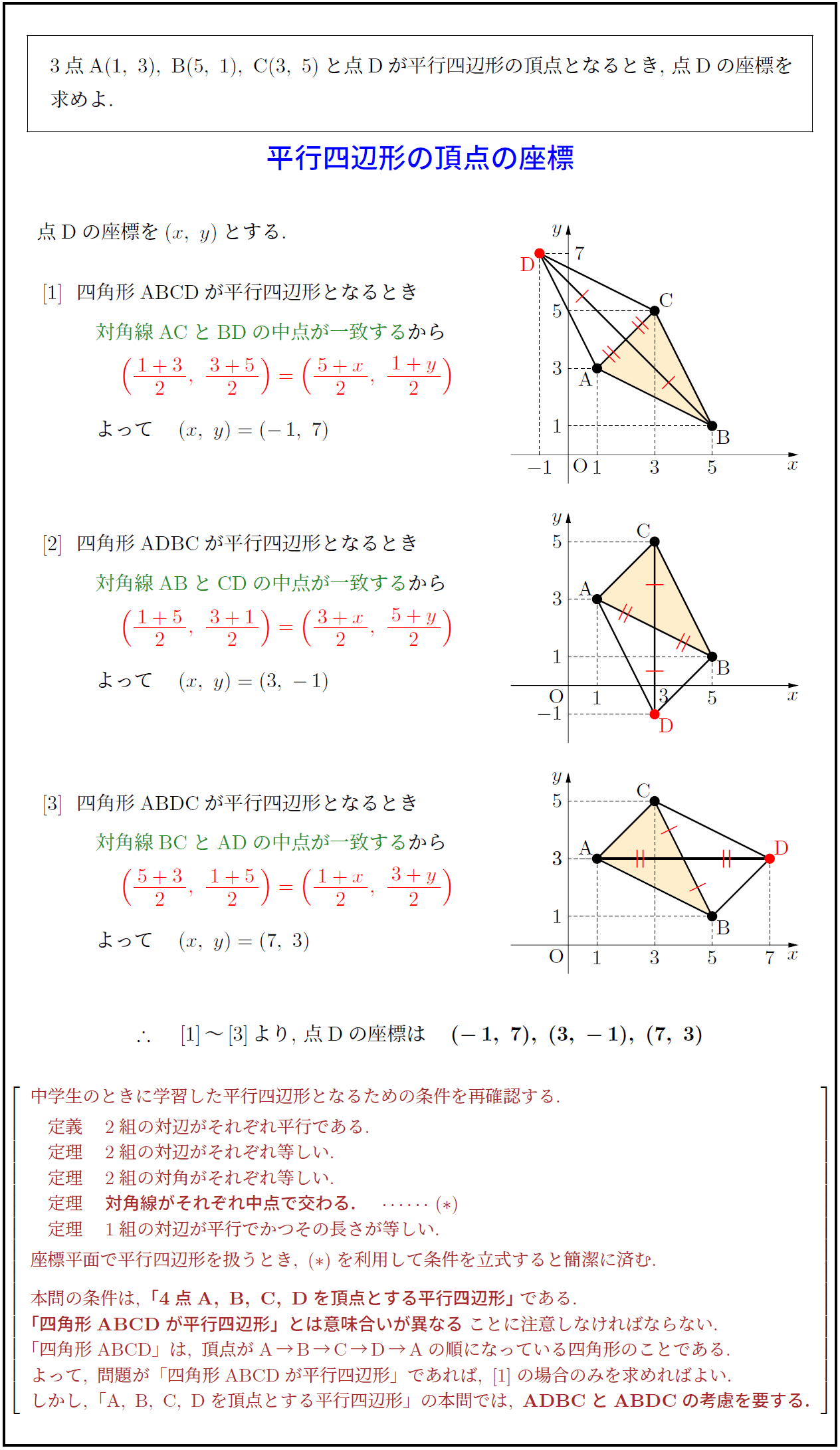
高校数学 平行四辺形の頂点の座標 受験の月

うさぎでもわかる線形代数 補充1 線形代数におけるベクトル 内積と外積 工業大学生ももやまのうさぎ塾

行列式の計算方法と図形的意味を解説してみる 線形代数を宇宙一わかりやすく解説してみるサイト

数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

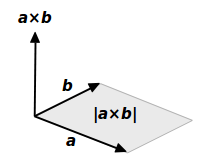
ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門

倍横距法を用いて多角形の面積を求める方法

ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門

2

勉強しよう数学3c エディントンのイプシロンと行列式とベクトルの外積

2

Fn 3次元空間における面の向きを調べる Flash テクニカルノート

ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示

平面幾何におけるベクトル演算 内積と外積

平行四辺形のベクトル 面積比の問題です 大学入試数学問題の解説 解答

高校数学b 平行六面体と空間ベクトルの演算 受験の月

ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門

Studydoctor空間座標と平行四辺形 数ｂ Studydoctor

ベクトル平行四辺形証明 位置ベクトルを利用して平行四辺形を Yahoo 知恵袋

1

外積を使って解く入試問題例 東大落ちの受験勉強法

新訂版序文の人 大類昌俊 Gvcuuchv 14 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで 平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な

外積の長さ 平行四辺形の面積 証明 理数アラカルト

エクセルのグラフで学ぶ気象学 補説０５

蛍光ペンを引いたところが分かりません どうしてその4つの面だけ平行四辺形であ Clearnote

ベクトルの外積 ２００７ 鎌田 Ppt Download

新訂版序文の人 大類昌俊 Gvcuuchv 14 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで 平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な

ベクトル方程式を超わかりやすく解説した 理系ラボ

物理のための数学 ベクトルの外積 お茶処やまと屋

平行四辺形の面積の２等分

平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clearnote

ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門

勉強しよう数学 べクトルの外積と複素数の積との関係を初めて学ぶ学び方

数b空間ベクトル 21年度京都大学文系数学4番 基本問題に潜む意外な落とし穴 学習村の 国公立へ行こう

行列式 方程式の解 Cramerの公式 余因数展開 Ppt Download

ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ

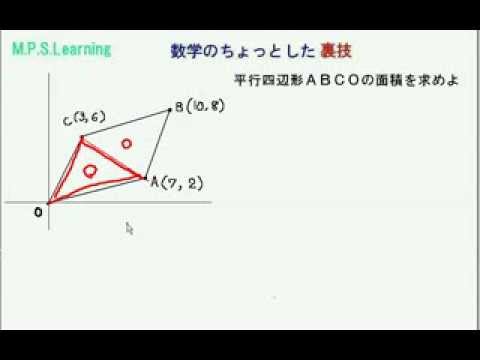
1次関数の応用 平行四辺形の面積 Youtube

高校数学b ベクトルの成分表示と平行四辺形 受験の月

平行四辺形の面積と行列式 Youtube

数学b ベクトルの範囲です 平行四辺形abcdの辺cdを3 1に内分する Yahoo 知恵袋

外積の長さ 平行四辺形の面積 証明 理数アラカルト

N点からなる多角形の面積を求める イメージングソリューション

3

標準 平行四辺形とベクトルの演算 なかけんの数学ノート

平行四辺形の面積の求め方 公式と計算例

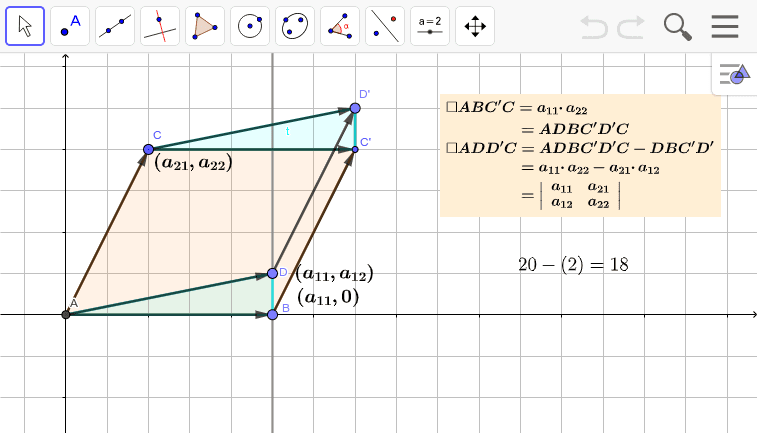
平行四辺形の面積と行列式 Geogebra

空間における平行四辺形の面積 外積 1 231頁 高卒で大学数学

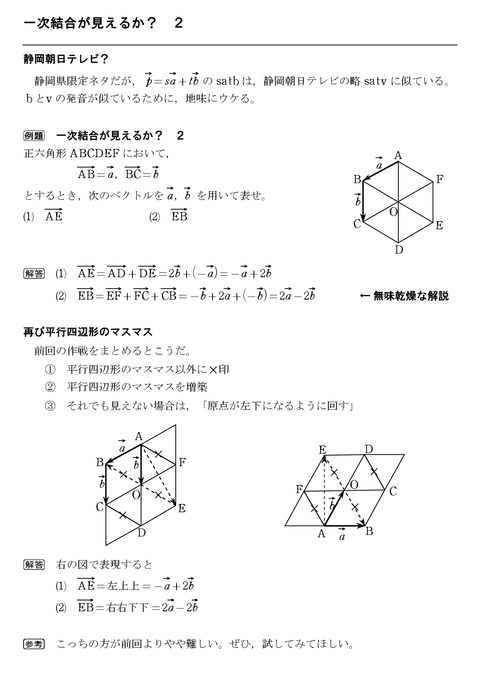
ベクトル 怜悧玲瓏 高校数学を天空から俯瞰する

曲線座標表示の一般論への補足その２ 平行四辺形の面積とベクトル外積 Jo3krpの独り言

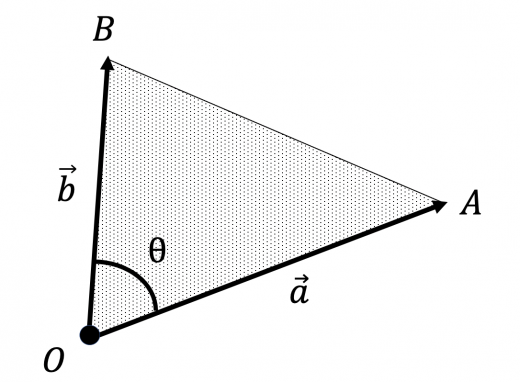
三角形の面積のベクトル 成分を用いた公式 高校数学の美しい物語

平行性変形でのベクトルの小手技

平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori

ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ

標準 ベクトルの成分と平行四辺形 なかけんの数学ノート

ねこ騙し数学

平行四辺形と螺子

平行 四辺 形 公式 3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく Tmh Io

数学iiic ベクトルの 外積 あるいは平行四辺形の面積

台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典

2次の正方行列式と平行四辺形の面積 機械学習に詳しくなりたいブログ

相似 平行四辺形と面積比の問題を徹底解説 数スタ

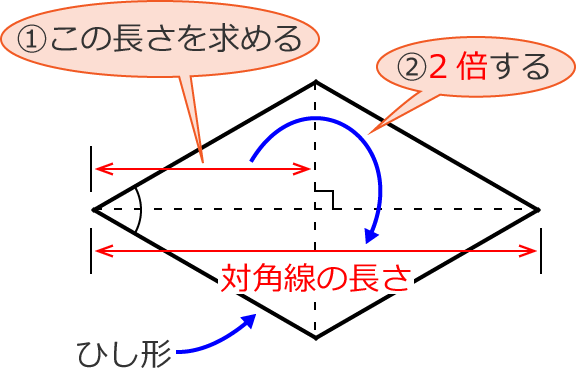
ひし形の対角線の長さの求め方

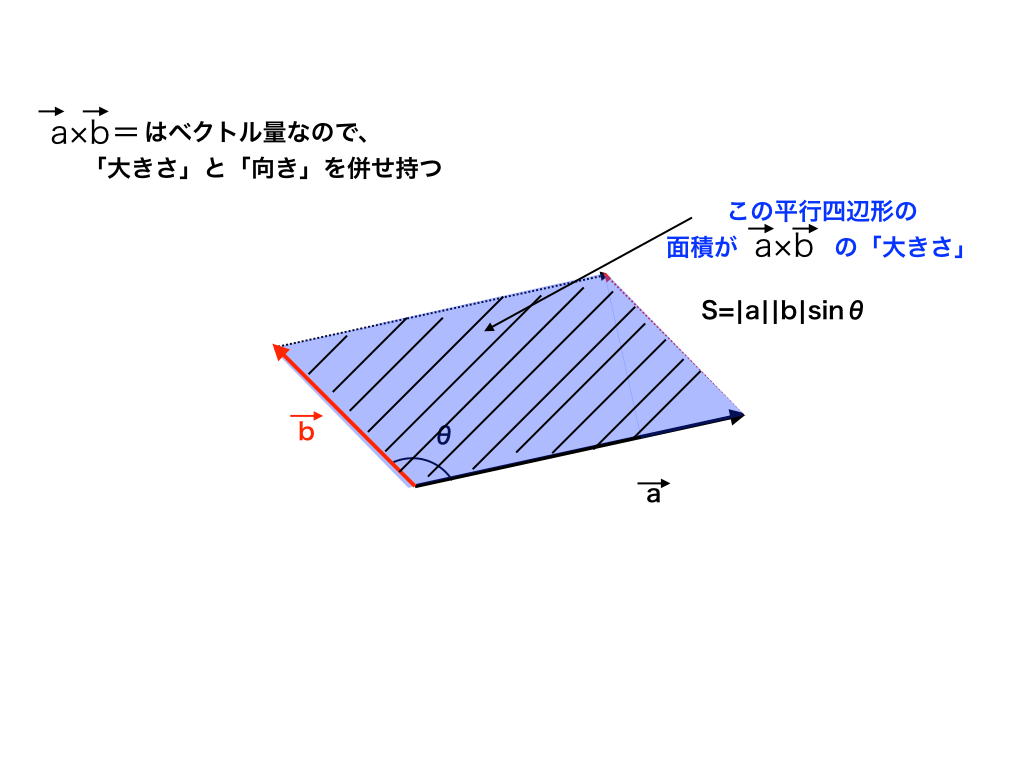
外積とは ベクトルの積の意味 計算法 公式をわかりやすく解説

Studydoctor平行四辺形と共線条件 数ｂ Studydoctor

勉強しよう数学 三角形の面積をベクトルで分解して計算する

2

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学

高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット

数学bの平行四辺形のベクトルの問題で 画像のof Odの答えの Yahoo 知恵袋

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

3

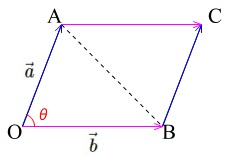
ベクトルの大きさと内積だけで表す面積の公式

四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題

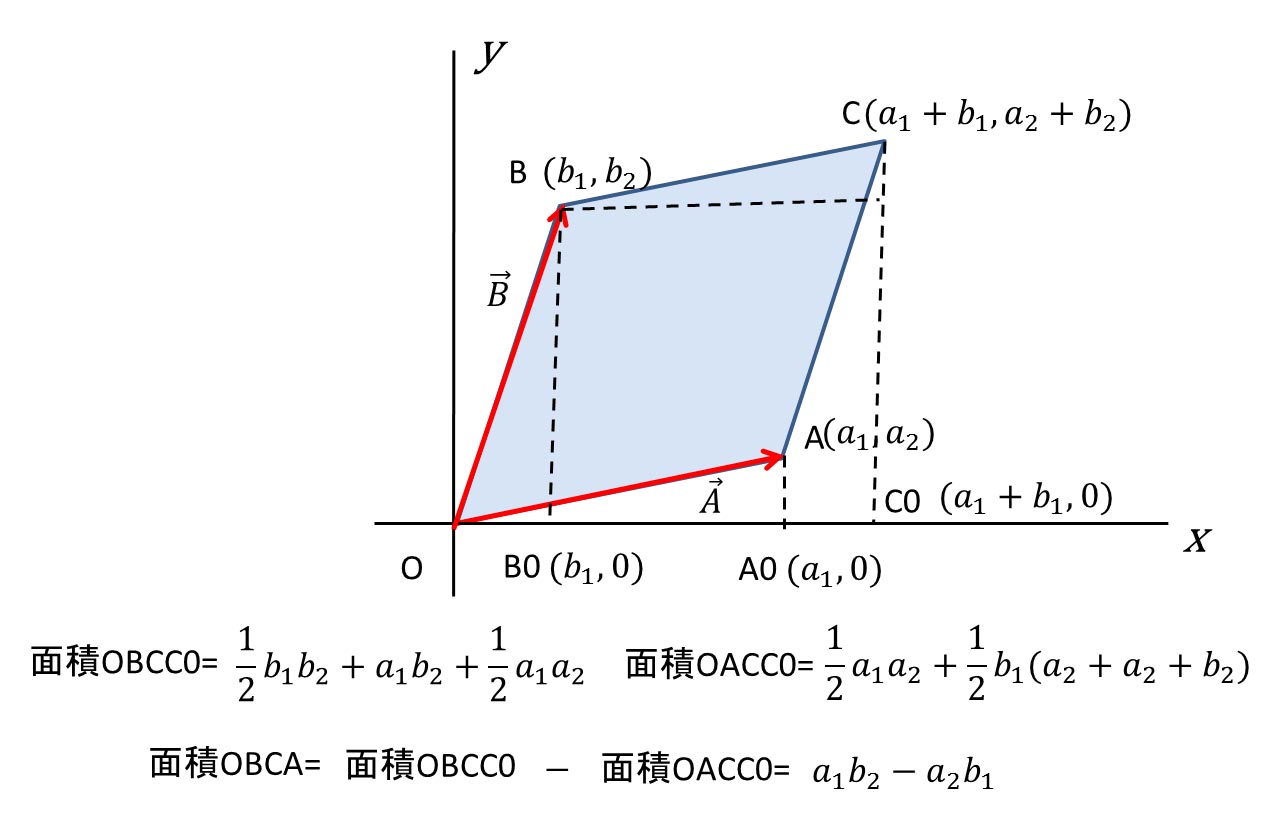
エクセルのグラフで学ぶ気象学 補説０５

2

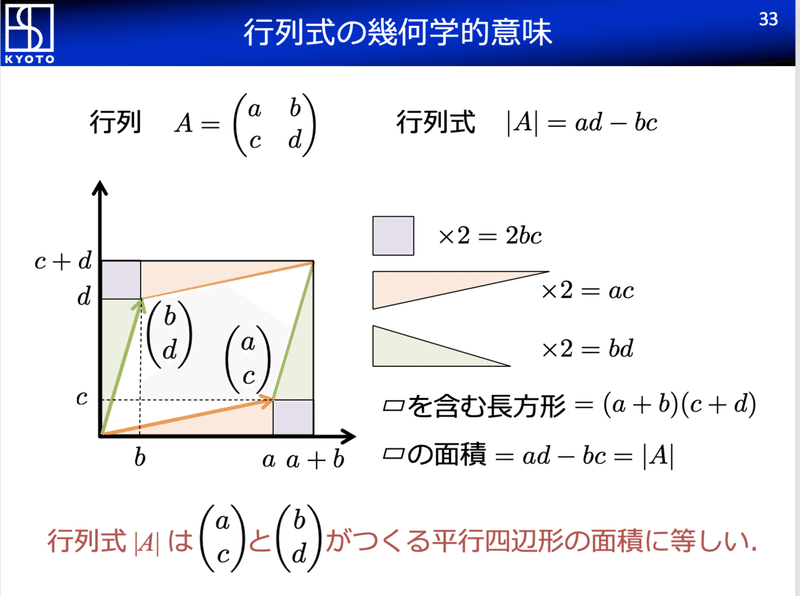
行列式 A Ad の幾何学的意味 Dr Kano Note

3 の平行四辺形の面積の求め方を教えてください 答えです 42 Clearnote

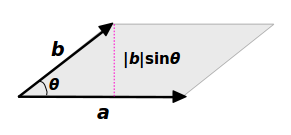
ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門

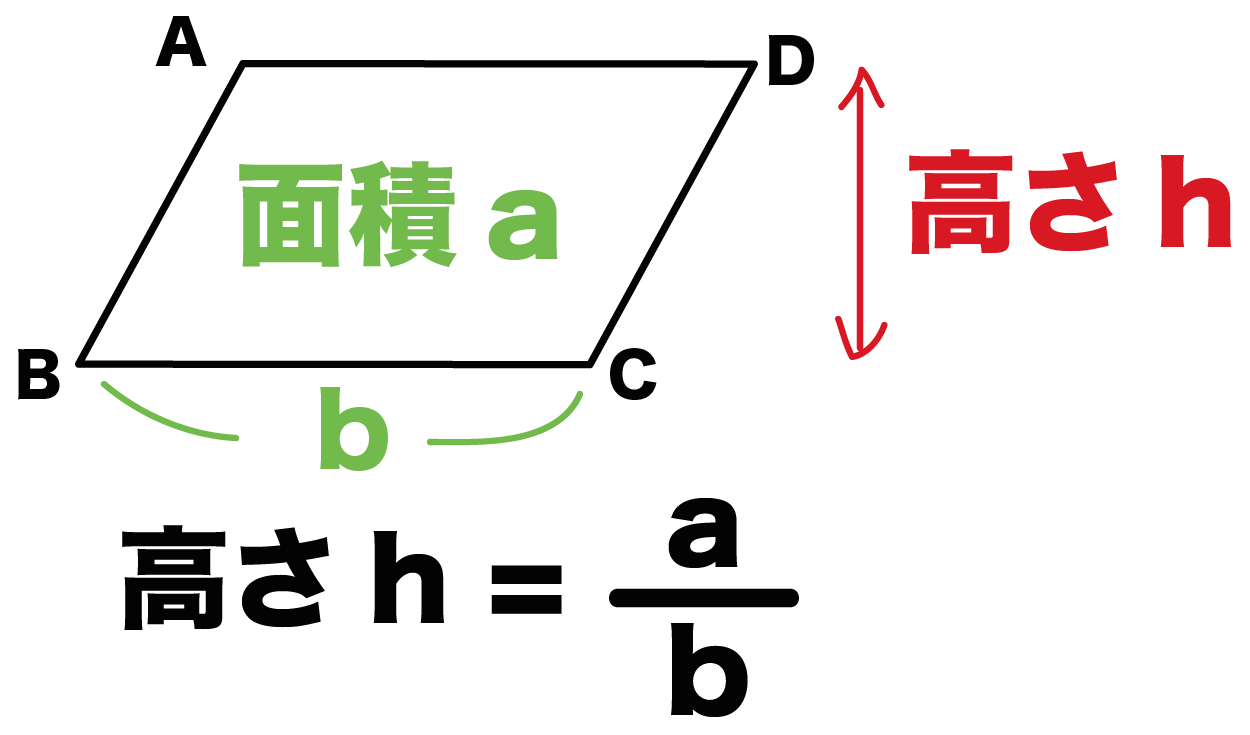
中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく

面積分

高校数学行列編 少しだけ線形代数 ダウンロード版 高橋直也塾数学物理 電験計量士教室 Booth

台形の面積の求め方 公式と計算例

8月 13 試行錯誤

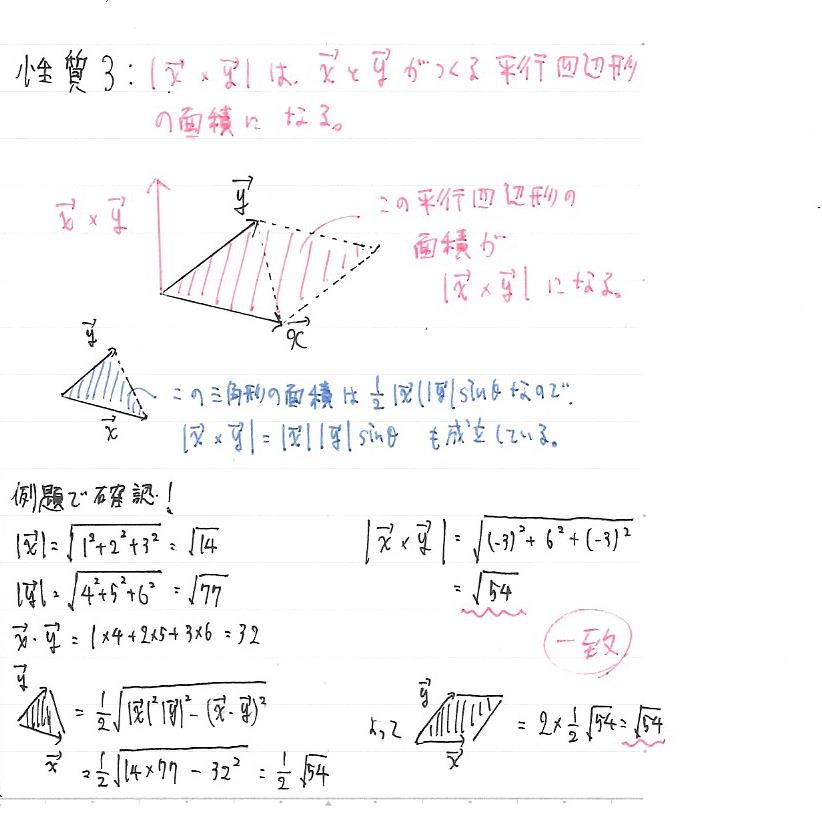
ベクトル 平行 四辺 形 面積 3つのベクトルの張る体積

行列式 線型代数 数学教育

1

ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張

Excelを使った数値計算ツールsuitexl

高校数学b 平行四辺形とベクトル 例題編 映像授業のtry It トライイット

Incoming Term: ベクトル 平行四辺形 面積 公式,